• 異常気象リスクマップとは
• はじめに
• 対象とする現象について
• 用いた観測データについて
• 大雨のリスクマップ
• 「30年に1回の大雨」「100年に1回の大雨」（確率降水量）
• 確率降水量とは
• 確率降水量の推定方法
• 「100年に1回の大雨」は何mmくらい？
• 「30年に1回の大雨」は何mmくらい？
• 日降水量100mm以上の大雨は年に何日降っている？
• 大雨が増えている
• 極端な多雨・少雨の年が増えている
• 少雨のリスクマップ
• 「10年に1回の少雨」は何mm？
• 参考
• 異常気象リスクマップのデータ
• 確率降水量に関するＱ＆Ａ

異常気象リスクマップ

確率降水量の推定方法

＊以下は、日降水量の確率降水量を例に解説していますが、24時間降水量についても同様の方法で推定しています。

確率降水量・再現期間は、観測値をもとに、確率分布を当てはめて推定しています。 また、確率分布は、５種類の中から、観測値と良く合っていて、計算結果が安定しているものを、地点ごとに選択しています。

１．観測値を使った計算のイメージ

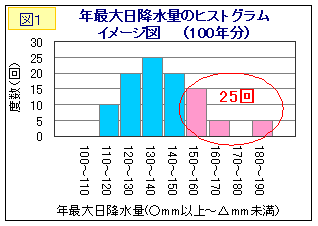
　図１は、ある地点の100年分の年最大日降水量のヒストグラム（イメージ）です。 例えば、150mm以上の雨は何年に１回起きたかを考えてみます。図１から、150mm以上となった回数は25回で、これが100年の間で起きたので、100÷25＝4で４年に１回の頻度で降ったことがわかります。これは、
[全面積]／[全面積－150mm未満の面積]…（１）
という計算をしています。
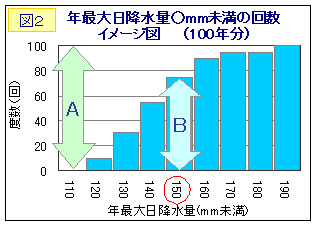
　次に、図１のヒストグラムの各階級の数を下から積算した図２の「○mm未満の回数」グラフで考えます。ここで再度150mm以上の雨が何年に１回起きたかを考えると、式（１）より
[A]÷[A－B]…（２）
で求めることができます。

２．確率分布を当てはめる

　実際には、図１のように、ある範囲の降水がたまたま観測されなかったり、逆に200年に１回並の大雨が100年のうちに観測されたりすることもあります。
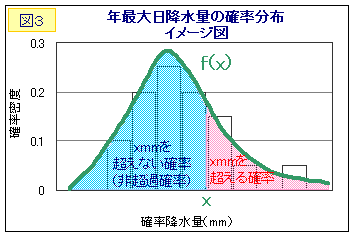
　そこで、図３の曲線のように、観測値の不自然な偏りを補正するような分布関数を当てはめてみます。全面積が１となるように規格化した分布関数をf(x)とすると、その面積は確率を意味します。
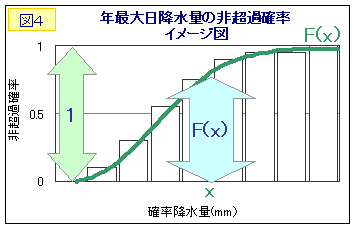
　ヒストグラムを下から積算した図２に対応するのが、f(x)を積分したF(x)です（図４）。日降水量xmmの再現期間T（ｘmmが何年に１回降ると推定されるか）は、式（２）より
T ＝１／（１－F(x)）
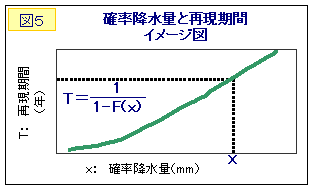
で求められます。また、T年の確率降水量ｘ（T年に１回の降水量は何mmと推定されるか）も、この式から逆算して求めることができます。 こうして、確率分布を当てはめることにより、図５のように、任意の確率降水量と再現期間を計算することができます。

３．使用している５種類の確率分布

　今回使用したのは、次の５種類の確率分布です。

• (1) グンベル分布
• (2) 一般化極値（ＧＥＶ）分布
• (3) 平方根指数型最大値分布
• (4) 対数ピアソンⅢ型分布
• (5) 対数正規分布

　(1)～(3)の３つは、極値理論（最大値や最小値に対する統計学的な理論）に基づく極値分布と呼ばれる分布です。残りの(4)と(5)は、極値分布とよく一致するため、従来から用いられている分布です。各年の最大値である「年最大日降水量」の観測値に、これらの分布を当てはめ、５種類の中から最適な分布を採用しました。

４．観測値と合っているかどうか

　観測値と合っているか（適合度）を見積もるため、SLSCという指標を用いています。
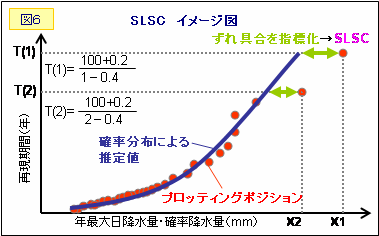
SLSCは、「観測値をプロッティングポジション公式で並べた場合」と、「確率分布から推定した場合」との確率降水量の差を指標化したものです。小さいほど適合度が良く、ここでは0.04以下で適合していると判断しています。
　プロッティングポジション公式とは、経験的に求められた公式で、観測値の個数・順位と再現期間との関係を数式化したものです。いくつかの式が提唱されていますが、ここでは、多くの分布系によく適合するカナンプロットを使います。

　例えば、年最大日降水量の観測値が100個あり、１番大きな値がX1mm、２番目がX2mmならば、X1mmの再現期間T(１)は167年、X2mmの再現期間T(２)は63年…と順に決まっていきます。

５．計算結果が安定しているかどうか

　現在までの観測値をランダムにピックアップしたり、今後観測値が追加されたりしても、結果が大きく変わらないことも、実用上、重要な条件となります。
この安定性を判断するために、ジャックナイフ法で評価を行っています。これは、N個のデータから、１つ目のデータを抜いたデータセット、２つ目のデータを抜いたデータセット…と、１個ずつのデータを抜いたN－1個のデータセットをN通り準備し、それぞれのデータセットから計算される確率降水量のばらつき(変動幅)を見る方法です。ばらつきの小さい方が安定しています。
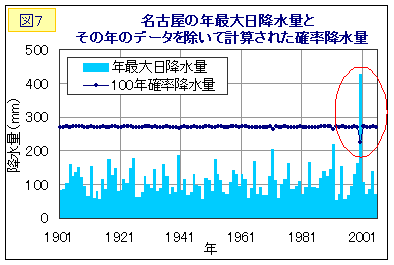
　極端に大きな観測値を抜いた時、確率降水量は大きく下がります。（図７は名古屋の確率降水量の計算において2000年の豪雨を抜いた例）

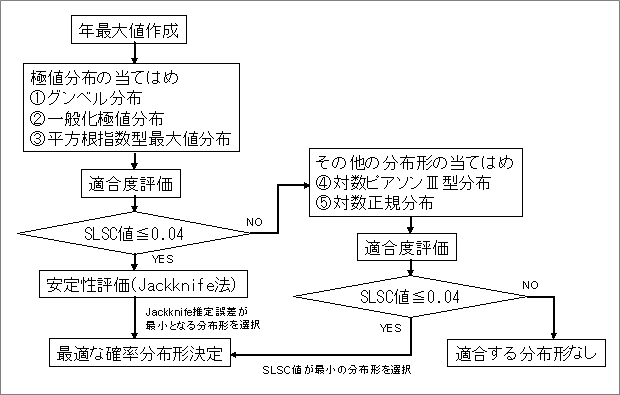
６．確率分布選択のフローチャート

　確率分布の選択は、平成11年に河川技術者、学識経験者等によって策定された「中小河川計画の手引き（案）」を基本としています。
　まず、極値分布の３種類の分布で、SLSCが0.04以下となる分布があれば、その中でジャックナイフ推定誤差の最も小さな分布を採用します。３種類の分布のSLSCが全て0.04より大きい場合は、残りの２種類の分布のうち、SLSCが0.04以下で小さい方を採用します。なお、５種類の確率分布形のSLSCが全て0.04より大きい場合は、最もSLSC値が小さいものを求め、適合度が基準を満たしていないことに留意した上で掲載することとします。